[TOC]
1.三门问题(Monty Hall problem)
亦称为蒙提霍尔问题或蒙提霍尔悖论,大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔(Monty Hall)。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机率?
作为工科生,还是拿贝叶斯公式来分析一波:
首先看贝叶斯公式:
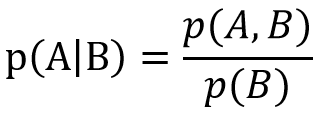
p(A|B)的意思是在B事件发生的情况下,A事件发生的概率。p(A,B)是两个事件同时发生的概率。
那么上面的公式可以延伸出下面的公式:
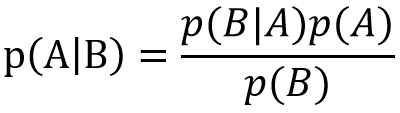
好,然后我们针对这个题目,我们假设有A、B、C三个门,参赛者选择了A门,主持人打开了B门,然后要参赛者在A门和C门之间抉择换还是不换。那么如果汽车在B门后面,换与不换得到汽车的概率均为0,如果换了能赢,那么汽车必须在C门后面, 现在我们求以下概率:
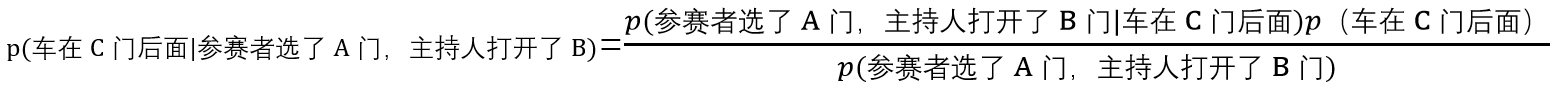
我们先看分母,我们三种可能情况列一下:

所以分母为:

再看分子,当车在C后面时,参赛者选择了A门,支持人只有B门可以打开,所以:
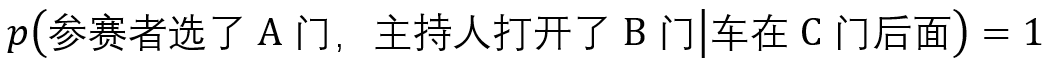
而车在C门后的概率显而易见:

然后我们就求得了换门获胜的概率:

-————————————————————————————————————————
这个问题就结束了。然而对于贝叶斯公式还没有结束。
贝叶斯公式还会有如下写法:
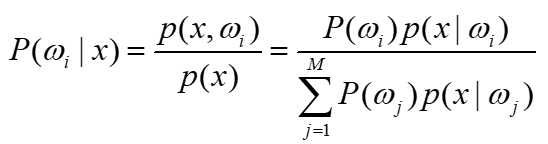
这个公式可以用在分类上,具体的可以去翻看我的另一篇博客
2.桶装水
有无限的水,5L和6L 的桶精确装4L 水
通用解法: 用小的桶不断往大桶填水
这里: 5L桶 6L桶
0 0
5 0
0 5
5 5
4 6
一个装了10L水的桶,一个7L的空桶,一个3L的空桶,怎样变成2个5L
初始时为10,0,0。
第二步7,0,3。
然后7,3,0。
然后4,3,3。
然后4,6,0。
然后1,6,3。
然后1,7,2。
然后8,0,2。
然后8,2,0。
然后5,2,3。
然后5,5,0。
如果你有无穷多的水,一个3夸脱的和一个5夸脱的提桶,你如何准确称出 4夸脱的水?
初始时0,5
然后3,2
然后0,2
然后2,0
然后2,5
然后1,4
两个舀酒的勺子,分别能舀7两和11两酒,二两酒?
初始0,11
然后7,4
然后0,4
然后4,0
然后4,11
然后7,8
然后0,8
然后7,1
然后0,1
-—–
然后1,11
然后7,5
然后0,5
然后5,0
然后5,11,
然后7,9
然后0,9
然后7,2
3.瞎子分牌
一副牌52张,告诉瞎子里面有10张牌是正面朝上的, 要求瞎子把这52张牌分成两堆, 并且每堆牌正面朝上的张数相同,可任意翻动牌,但是一直不可以看。
分成10和42, 10 中的所有牌。
proof: 第一堆(10张牌里有x张向上),全翻 = 10-x 张向上,等于第二堆向上的牌数
4.赛马问题
A1>A2>A3>A4
B1>B2>B3>B4
C1>C2>C3>C4
64匹马,8个跑道,选跑最快的4匹马需要比赛多少次。
第一步:首先每8匹马跑一次,总共需要8次,假设结果中A1>A2>A3>……,B1>B2>B3>….等。 sum=8;
第二步:这8组中的第一名拉出来跑一次,那么这次最快的是总的第一名,假设是A1,同时假设B1>C1>D1。这时还要角逐2,3,4名, 那这一轮中的第五到第八组都可以直接舍弃 ,因为他们所有的马一定进不了前4名。sum=9。
第三步:从A组中选A2,A3,A4,B组中B1,B2,B3,C组中C1,C2,D组中D1,这些才有资格角逐2,3,4名。这时需要再比赛两次。 sum=11。(但是如果第10轮选择A4不上场,如果A3获得了第4名,那么A4就不需要比赛了,这样 sum=10 )。
25匹马,5个跑道,每个跑道最多能有1匹马进行比赛,最少比多少次能比出前3名?前5名?
5.老鼠死亡问题
1000瓶药,有一些可能有毒,用老鼠来喝药,喝到有毒的一周就死。一周内至少需要多少只老鼠才能检测到哪些有毒
同时给老鼠编号,从1,2,…10,从低位开始,让第n个编号老鼠喝下第n个bit位为1的瓶子中的药水。
一周后,若所有的老鼠都没有发病,那么是第0个瓶子有毒,
如果有一些编号的老鼠发病,死亡的老鼠记为1,正常老鼠记为0,那么按照老鼠编号1-10对应bit位从低到高,对应的10进制即为有毒药水的编号。
附上百度解释
给1000个瓶分别标上如下标签(10位长度):
0000000001 (第1瓶)
0000000010 (第2瓶)
0000000011 (第3瓶)
……
1111101000 (第1000瓶)
从编号最后1位是1的所有的瓶子里面取出1滴混在一起(比如从第一瓶,第三瓶,。。。里分别取出一滴混在一起)并标上记号为1。以此类推,从编号第一位是1的所有的瓶子里面取出1滴混在一起并标上记号为10。现在得到有10个编号的混合液,小白鼠排排站,分别标上10,9,。。。1号,并分别给它们灌上对应号码的混合液。24小时过去了,过来验尸吧:
从左到右,死了的小白鼠贴上标签1,没死的贴上0,最后得到一个序号,把这个序号换成10进制的数字,就是有毒的那瓶水的编号。
检验一下:假如第一瓶有毒,按照0000000001 (第1瓶),说明第1号混合液有毒,因此小白鼠的生死符为0000000001(编号为1的小白鼠挂了),0000000001二进制标签转换成十进制=1号瓶有毒;假如第三瓶有毒,0000000011 (第3瓶),第1号和第2号混合液有毒,因此小白鼠的生死符为00000011(编号为1,2的鼠兄弟挂了),0000000011二进制标签转换成十进制=3号瓶有毒。
————————————————————————————————————————————
举例,10瓶药水,4个bit表示,对应药水编号0-9,又4个bit对应4个老鼠,则老鼠编号1-4,
0000, 0
0001, 1
0010, 2
0011, 3
0100, 4
0101,5
0110,6
0111,7
1000,8
1001,9
老鼠编号 对应药水瓶子编号
1, ,,, 1,3,5,7,9
2, ,,, 2,3,6,7
3, ,,,4,5,6,7
4, ,,,8,9
如果一周之后,全都安然无恙,则0号药水瓶子有毒,
如果1,2,3编号老鼠死亡,则很容易看出7号有毒,
或者1,2,3编号老鼠置为1,4号置为0,从低到高即为0111=7
6.石头称重
13个石头,有一个比较重其他都一样,用天平测量最多需要几次才能测出重的那个
4 4 5
1) 如果 4 == 4 在 5 里面 分为 2 2 1
1.1) 如果 2 == 2 在 1 那 ok 两次
1.2) 如果 2 != 2 称 1 1 ,那个沉就是答案,三次
2) 4 != 4 在 沉的那堆里面
2.1) 称2 2 排除 2个 再称1 1 ,那个沉就是答案,三次
7.抛硬币
一硬币,一面向上概率0.7,一面0.3,如何公平?
两个人轮流抛硬币,先抛到正面的赢,问先抛的人赢的概率?
每一轮 抛硬币,A先抛赢得概率是1/2,B后抛赢得概率是(1/2)*(1/2)= 1/4。那么 每一轮A赢得概率都是B赢得概率的2倍 ,总概率为1,所以A赢的概率是2/3。
8.蚊香
两根香,一根烧完1小时,如何测量15分钟
开始时一根香两头点着,一根香只点一头,两头点着的香烧完说明过去了半小时,这时将只点了一头的香另一头也点着,从这时开始到烧完就是15分钟。
9.海盗分金币
1.
在加勒比海上,有五个海盗,共同抢到了100枚金币, 每一个人按顺序依次提出自己的分配方案,如果提出的方案没有获得半数或半数以上的人的同意,则这个提出方案的人就被扔到海里喂鲨鱼,那么第一个提出方案的人要怎么做,才能使自己的利益最大化?(前提是海盗都是十分聪明和贪婪的)
假使前三个人都因为分配金币的方式不合理而被扔下大海,此时还剩下两个人,也就是4号和5号,那么问题就简单了:
4号和5号分金币的情况:
4号提出方案,自己一定会同意的,并且只要自己同意,这个方案就已经获得了半数的支持,就可以被实施
因此,无论5号是否同意4号提出的方案,都不会对最终的结果造成影响,因此,4号一定会要100枚金币,以使自己的利益最大化,结果就变成了这样:
4号 5号
100 0
现在我们多添加一个人,
3号,4号和5号分金币的情况:
3号要使自己的提议获得半数的支持就必须再拉拢一个人,拉拢4号显然是不合适的,4号一定不会同意,4号知道,只要搞死了3号,剩下的100枚金币都是自己的。(就像上面4号和5号分金币的情况)拉拢5号是合适的,因为5号之前得不到金币,现在只要3号给5号一个金币就能够获得5号的支持,因为5号也知道,如果3号死亡,自己一定一枚金币都得不到。
情况就变成了这样:
3号 4号 5号
99 0 1
现在我们再多添加一个人:
2号,3号,4号和5号分金币的情况:
2号要使自己的提议获得半数的支持也必须再拉拢一个人,拉拢3号显示是不合适的,3号一定不会同意,3号知道,只要搞死了2号,有99枚金币都是自己的(就像上面3号,4号和5号分金币的情况), 拉拢5号貌似是可以的,他已经有一个金币了,要让他支持自己只要再多给他一个金币就可以了,拉拢4号也是可以的,4号现在没有金币,只要给他一个就可以让他自持自己的提案,综上所述,要让自己利益最大化,就需要拉拢4号,因为只要给4号一个金币即可:
情况就变成了这样:
2号 3号 4号 5号
99 0 1 0
最后我们再多添加一个人这道题目的答案就出来了:
1号,2号,3号,4号和5号分金币的情况:
1号要使自己的提议获得半数的支持必须拉拢两个人,拉拢2号显示是不合适的,2号一定不会同意,2号知道,只要搞死了1号,有99枚金币都是自己的,(就像上面2号,3号,4号和5号分金币的情况), 拉拢4号貌似是可以的,他已经有一个金币了,要让他支持自己需要再给他一个金币才可以,这样做并不能让自己的利益最大化, 拉拢3号是可以的,3号现在没有金币,只要给他一个就可以让他自持自己的提案, 5号跟3号情况一至,同样没有金币,只要给他一个就可以了,综上所述,要让自己利益最大化,就需要拉拢3号跟5号,因为拉拢他们两个只需要各自给一个金币即可:
情况就变成了这样:
1号 2号 3号 4号 5号
98 0 1 0 1
或必须半数以上的人同意呢?
这道题是典型的逆向思维的问题,用回推法可以得到答案。过程如下:从后往前推,人数依次增加如果1-3号强盗都喂了鲨鱼,只剩4号和5号的话,5号一定投反对票让4号喂鲨鱼,以独吞全部金币。所以,4号惟有支持3号才能保命。3号知道这一点,就会提(100,0,0)的分配方案,对4号、5号一毛不拔而将全部金币归为已有,因为他知道4号一无所获但还是会投赞成票,再加上自己一票,他的方案即可通过。2号推到3号的方案,就会提出(98,0,1,1)的方案,即放弃3号,而给予4号和5号各一枚金币。由于该方案对于4号和5号来说比在3号分配时更为有利,他们将支持他而不希望他出局而由3号来分配。这样,2号将拿走98枚金币。2号的方案会被1号所洞悉,1号并将提出(97,0,1,2,0)或(97,0,1,0,2)的方案,即放弃2号,而给3号一枚金币,同时给4号(或5号)2枚金币。由于1号的这一方案对于3号和4号(或5号)来说,相比2号分配时更优,他们将投1号的赞成票,再加上1号自己的票,1号的方案可获通过,97枚金币可轻松落入囊中。这无疑是1号能够获取最大收益的方案了!
10. 54张扑克牌,平均分成3份,大小王在一份的概率
首先大王一定会在某一份中,然后要计算这一份中还要包含小王的概率。去掉大王还剩53张牌,这一份还可以分17张牌,那么每次分到小王的概率是1/53,所以总概率是17/53。
11.让你设计一个微信发红包的api,你会怎么设计,不能有人领到的红包里面没钱,红包数值精确到分。
传入参数有总钱数,分的份数,随机分还是等分。先判断钱数能不能分那么多份,这个直接用总钱数>=0.01份数判断就可以了。然后根据分发策略,选择随机还是等分,随机的话就给 1到总钱数-(总份数-1)0.01 的随机数(总钱数以分为单位),等分的话直接除判断能不能除开,有余数就将余数加到最后一份里面。
12.分布式多个机器生成id,如何保证不重复?
\1. snowflake方案 :
snowflake是Twitter开源的分布式ID生成算法,结果是一个long型的ID。其核心思想是:使用41bit作为毫秒数,10bit作为机器的ID(5个bit是数据中心,5个bit的机器ID),12bit作为毫秒内的流水号(意味着 每个节点在每毫秒可以产生 4096 个 ID ),最后还有一个符号位,永远是0。
优点 :
1.毫秒数在高位,自增序列在低位,整个ID都是趋势递增的。
2.不依赖数据库等第三方系统,以服务的方式部署,稳定性更高,生成ID的性能也是非常高的。
3.可以根据自身业务特性分配bit位,非常灵活。
缺点 :
强依赖机器时钟,如果 机器上时钟回拨 ,会导致发号重复或者服务会处于不可用状态。
\2. 用Redis生成ID:
因为Redis是单线程的,也可以用来生成全局唯一ID。可以用Redis的原子操作INCR和INCRBY来实现。
此外,可以使用Redis集群来获取更高的吞吐量。假如一个集群中有5台Redis,可以初始化每台Redis的值分别是1,2,3,4,5,步长都是5,各Redis生成的ID如下:
A:1,6,11,16
B:2,7,12,17
C:3,8,13,18
D:4,9,14,19
E:5,10,15,20
这种方式是负载到哪台机器提前定好,未来很难做修改。3~5台服务器基本能够满足需求,都可以获得不同的ID,但步长和初始值一定需要事先确定,使用Redis集群也可以解决单点故障问题。
另外,比较适合使用Redis来生成每天从0开始的流水号,如订单号=日期+当日自增长号。可以每天在Redis中生成一个Key,使用INCR进行累加。
优点:
1)不依赖于数据库,灵活方便,且性能优于数据库。
缺点:
1)如果系统中没有Redis,需要引入新的组件,增加系统复杂度。
2)需要编码和配置的工作量较大。
13.数据库连接池怎么设计?
需要考虑的问题:
- 限制连接池中最多、可以容纳的连接数目,避免过度消耗系统资源。
- 当客户请求连接,而连接池中所有连接都已被占用时,该如何处理呢?一种方式是让客户一直等待,直到有空闲连接,另一种方式是为客户分配一个新的临时连接。
- 当客户不再使用连接,需要把连接重新放回连接池。
- 连接池中允许处于空闲状态的连接的最大项目。假定允许的最长空闲时间为十分钟,并且允许空闲状态的连接最大数目为5,
那么当连接池中有n个(n>5)连接处于空闲状态的时间超过十分钟时, 就应该把n-5个连接关闭,并且从连接池中删除, 这样才能更有效的利用系统资源。
14.扫码登录
15.砝码秤盐
140g盐,一天平,7g 、2g砝码各一个,如何只利用这些东西3次把盐分成50g和90g?
第一次: 7g、2g砝码称出9g盐,结果盐分成9g与131g
第二次:将9g盐与7g、2g都作为砝码,结果将盐分为18g与113g (注意:这时盐已经分为三份:9g、18g、113g,还有两个砝码)
第三次:将18g盐与7g砝码发在左托盘,将2g砝码放在右托盘,然后在113g盐中取盐添置右托盘中,可获取23g盐。
这时盐分为9g,18g,23g与90g。
即三次,可以得到90g与(9+18+23)50g。
16.九球称重
有 9 个球,其中 8 个球质量相同,有 1 个球比较重。要求用 2 次天平,找出比较重的那个球。
将这些球均分成 3 个一组共 3 组,选出 2 组称重,如果 1 组比较重,那么重球在比较重的那 1 组;如果 1 组重量相等,那么重球在另外 1 组。
对比较重的那 1 组的 3 个球再分成 3 组,重复上面的步骤。
17.药丸称重
有 20 瓶药丸,其中 19 瓶药丸质量相同为 1 克,剩下一瓶药丸质量为 1.1 克。瓶子中有无数个药丸。要求用一次天平找出药丸质量 1.1 克的药瓶。
可以从药丸的数量上来制造差异:从第 i 瓶药丸中取出 i 个药丸,然后一起称重。可以知道,如果第 i 瓶药丸重 1.1 克/粒,那么称重结果就会比正常情况下重 0.1 * i 克。
18.得到 4 升的水
有两个杯子,容量分别为 5 升和 3 升,水的供应不断。问怎么用这两个杯子得到 4 升的水。
- 1、将3升的装满倒入5升的;
2、再一次将3升的转满,倒入5升的,把5升装满;
3、3升杯里剩下的就是1升水;
4、倒掉5升的,把1升水倒入5升杯;
5、第三次加满3升杯,倒入5升杯,得到4升水。
19.扔鸡蛋
一栋楼有 100 层,在第 N 层或者更高扔鸡蛋会破,而第 N 层往下则不会。给 2 个鸡蛋,求 N,要求最差的情况下扔鸡蛋的次数最少
X
最优解法是反向思考的经典:如果最优解法在最坏情况下需要扔X次,那第一次在第几层扔最好呢?
答案是:从X层扔
假设最优的尝试次数的x次,为什么第一次扔就要选择第x层呢?
这里的解释会有些烧脑,请小伙伴们坐稳扶好:
假设第一次扔在第x+1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x层。
这样一来,我们总共尝试了x+1次,和假设尝试x次相悖。由此可见,第一次扔的楼层必须小于x+1层。
假设第一次扔在第x-1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-2层。
这样一来,我们总共尝试了x-2+1 = x-1次,虽然没有超出假设次数,但似乎有些过于保守。
假设第一次扔在第x层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-1层。
这样一来,我们总共尝试了x-1+1 = x次,刚刚好没有超出假设次数。
因此,要想尽量楼层跨度大一些,又要保证不超过假设的尝试次数x,那么第一次扔鸡蛋的最优选择就是第x层。
那么算最坏情况,第二次你只剩下x-1次机会,从100-x层 扔
按照上面的说法,你第二次尝试的位置必然是X+(X-1);
以此类推我们可得:
x + (x-1) + (x-2) + … + 1 = 100
这个方程式不难理解:
左边的多项式是各次扔鸡蛋的楼层跨度之和。由于假设尝试x次,所以这个多项式共有x项。
右边是总的楼层数100。
下面我们来解这个方程:
x + (x-1) + (x-2) + … + 1 = 100 转化为
(x+1)*x/2 = 100
最终x向上取整,得到 x = 14
因此,最优解在最坏情况的尝试次数是14次,第一次扔鸡蛋的楼层也是14层。
最后,让我们把第一个鸡蛋没碎的情况下,所尝试的楼层数完整列举出来:
14,27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
举个栗子验证下:
假如鸡蛋不会碎的临界点是65层,那么第一个鸡蛋扔出的楼层是14,27,50,60,69。这时候啪的一声碎了。
第二个鸡蛋继续,从61层开始,61,62,63,64,65,66,啪的一声碎了。
因此得到不会碎的临界点65层,总尝试次数是 6 + 6 = 12 < 14 。
下面是我个人的理解:这个更像是优化版的均匀法,均匀法让你第二次尝试不超过10,但是第一次的位置无法保证(最多要9次,最好一次),这个由于每多一次尝试,楼层间隔就-1,最终使得第一次与第二次的和完全均匀(最差情况)。
但是核心思路是逆向思考,因为即使理解了需要两次的和均匀也很难得到第一次要在哪层楼扔。
一旦理解了这种方法,多少层楼你都不会怕啦~
来源:https://blog.csdn.net/qq_38316721/article/details/81351297
20.一个家庭有两个小孩,其中有一个是女孩,问另一个也是女孩的概率(假定生男生女的概率一样
1/3
样本空间为(男男)(女女)(男女)(女男)
A=(已知其中一个是女孩)=)(女女)(男女)(女男)
B=(另一个也是女孩)=(女女)
于是P(B/A)=P(AB)/P(A)=(1/4)/(3/4)=1/3
21.分金条
有个商人雇用了一位手艺高超的工匠了为他做一个精致产品,工作一星期七天的代价是一条金条。商人手头上有一条金条,刚好有可以付工匠一星期的工钱。但工匠要求工钱要按每天来付。虽然他并不急着用钱,每天有钱进账,老人心里总是踏实一些。但商人家中有个规矩,金条每星期只能切二刀。后来商人想出以了个切割金条的办法,满足了工匠的要求。你知道商人是怎么切割金条才能满足工匠的吗?
切成1、2、4。这三个二进制数的组合能表示0-7中的任何一个。
22.假钱问题
老王30买了双鞋,35卖,客人花100买,老王没零钱于是向老李换了100.补给客人后,客人走远后老李突然说是假钱,于是老王补偿给了老李,问老王一共亏了多少?
卖鞋赚了35-30=5
假钱赔了100
一共亏95
23.取硬币问题
30枚面值不全相同的硬币摆成一排,甲、乙两个人轮流选择这排硬币的其中一端,并取走最外边的那枚硬币。如果你先取硬币,能保证得到的钱不会比对手少吗?
先取者可以让自己总是取奇数位置上的硬币或者总是取偶数位置上的硬币。数一数是奇数位置上的面值总和多还是偶数位置上的面值总和多,然后总是取这些位置上的硬币就可以了。
24.旅馆问题
有三个人去住旅馆,住三间房,每一间房10元,于是他们一共付给老板30,第二天,老板觉得三间房只需要25元就够了 叫小弟退回5给三位客人,谁知小弟贪心,只退回每人1,自己偷偷拿了2,这样一来便等于那三位客人每人各花了九元,于是三个人一共花了27,再加上小弟独吞了2,总共是29。可是当初他们三个人一共付出30,那么还有剩下的1呢?
他们所消费的27元里已经包括小弟贪污的2元了,再加退还的3元=30元。:这30元现在的分布是:老板拿25元,伙计拿2元,三人各拿1元,正好!
25.蓝眼睛问题
有个岛上住着一群人,有一天来了个游客,定了一条奇怪的规矩:所有蓝眼睛的人都必须尽快离开这个岛。每晚8点会有一个航班离岛。每个人都看得见别人眼睛的颜色,但不知道自己的(别人也不可以告知)。此外,他们不知道岛上到底有多少人是蓝眼睛的,只知道至少有一个人的眼睛是蓝色的。所有蓝眼睛的人要花几天才能离开这个岛?
c=1
假设岛上所有人都是聪明的,蓝眼睛的人四处观察之后,发现没有人是蓝眼睛的。但他知道至少有一人是蓝眼睛的,于是就能推导出自己一定是蓝眼睛的。因此,他会搭乘当晚的飞机离开。
c=2
两个蓝眼睛的人看到对方,并不确定c是1还是2,但是由上一种情况,他们知道,如果c = 1,那个蓝眼睛的人第一晚就会离岛。因此,发现另一个蓝眼睛的人仍在岛上,他一定能推断出c = 2,也就意味着他自己也是蓝眼睛的。于是,两个蓝眼睛的人都会在第二晚离岛。
c>2
逐步提高c时,我们可以看出上述逻辑仍旧适用。如果c = 3,那么,这三个人会立即意识到有2到3人是蓝眼睛的。如果有两人是蓝眼睛的,那么这两人会在第二晚离岛。因此,如果过了第二晚另外两人还在岛上,每个蓝眼睛的人都能推断出c = 3,因此这三人都有蓝眼睛。他们会在第三晚离岛。
不论c为什么值,都可以套用这个模式。所以,如果有c人是蓝眼睛的,则所有蓝眼睛的人要用c晚才能离岛,且都在同一晚离开。
26.疯狗问题
有50家人家,每家一条狗。有一天警察通知,50条狗当中有病狗,行为和正常狗不一样。每人只能通过观察别人家的狗来判断自己家的狗是否生病,而不能看自己家的狗,如果判断出自己家的狗病了,就必须当天一枪打死自己家的狗。结果,第一天没有,第二天没有,第三天开始一阵枪响,问:一共死了几条狗?
死了3条(第几天枪响就有几条)。
从有一条不正常的狗开始,显然第一天将会听到一声枪响。这里的要点是你只需站在那条不正常狗的主人的角度考虑。
有两条的话思路继续,只考虑有两条不正常狗的人,其余人无需考虑。通过第一天他们了解了对方的信息。第二天杀死自己的狗。换句话说每个人需要一天的时间证明自己的狗是正常的。有三条的话,同样只考虑那三个人,其中每一个人需要两天的时间证明自己的狗是正常的狗。
27.耳光问题(跟蓝眼睛一样)
一群人开舞会,每人头上都戴着一顶帽子。帽子只有黑白两种,黑的至少有一顶。每个人都能看到其他人帽子的颜色,却看不到自己的。主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就打自己一个耳光。第一次关灯,没有声音。于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。一直到第三次关灯,才有劈劈啪啪打耳光的声音响起。问有多少人戴着黑帽子?
答案:有三个人戴黑帽。假设有N个人戴黑帽,当N=1时,戴黑帽的人看见别人都为白则能肯定自己为黑。于是第一次关灯就应该有声。可以断定N>1。对于每个戴黑帽的人来说,他能看见N-1顶黑帽,并由此假定自己为白。但等待N-1次还没有人打自己以后,每个戴黑人都能知道自己也是黑的了。所以第N次关灯就有N个人打自己。
28.红球篮球
你有两个罐子,每个罐子各有若干红色弹球和蓝色弹球,两个罐子共有50个红色弹球,50个蓝色弹球,随机选出一个罐子,随机从中选取出一个弹球,要使取出的是红球的概率最大,一开始两个罐子应放几个红球,几个蓝球?在你的计划中,得到红球的准确几率是多少?
一个罐子放1红,一个罐子放49红和50蓝,这样得到红球的概率接近3/4。
29.猜数字
教授选出两个从2到9的数,把它们的和告诉学生甲,把它们的积告诉学生乙,让他们轮流猜这两个数, 甲说:“我猜不出”, 乙说:“我猜不出”, 甲说:“我猜到了”, 乙说:“我也猜到了”, 问这两个数是多少?
3和4。设两个数为n1,n2,n1> =n2,甲听到的数为n=n1 n2,乙听到的数为m=n1*n2,证明n1=3,n2=4是唯一解。
证明:要证以上命题为真,不妨先证n=7
1)必要性:
i) n> 5 是显然的,因为n <4不可能,n=4或者n=5甲都不可能回答不知道
ii) n> 6 因为如果n=6的话,那么甲虽然不知道(不确定2 4还是3 3)但是无论是2,4还是3,3乙都不可能说不知道(m=8或者m=9的话乙说不知道是没有道理的)
iii) n <8 因为如果n> =8的话,就可以将n分解成 n=4 x 和 n=6 (x-2),那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10,那样n又可以分解成8 2,所以总之当n> =8时,n至少可以分解成两种不同的合数之和,这样乙说不知道的时候,甲就没有理由马上说知道。以上证明了必要性。
2)充分性
当n=7时,n可以分解成2 5或3 4
显然2 5不符合题意,舍去,容易判断出3 4符合题意,m=12,证毕
于是得到n=7 m=12 n1=3 n2=4是唯一解。
30.水果标签问题
3个箱子里面放了 苹果,梨子,苹果加梨子,标签全错误,只能选择查看一箱的水果来改正所有标签
查看贴苹果和梨标签那一个,如果拿出来的是苹果,代表这一箱只有苹果,因为如果是苹果和梨就代表标签没错了。
那么剩下的两箱就是梨,苹果和梨,剩下的标签是梨,苹果,由于标签全错,所以贴着苹果的是梨,贴着梨的是苹果和梨。
如果拿出来的是梨,同理代表这一箱只有梨。那么剩下的两箱就是苹果,苹果和梨,剩下的标签就是苹果,梨。由于标签全错,贴着苹果的就是苹果和梨,贴着梨的就是苹果。
31.便士标签问题(和水果标签一样)
假设在桌上有三个密封的盒,一个盒中有2枚银币(1银币=10便士),一个盒中有2枚镍币(1镍币=5便士),还有一个盒中有1枚银币和1枚镍币。这些盒子被标上10便士、 15便士和20便士,但每个标签都是错误的。允许你从一个盒中拿出1枚硬币放在盒前,看到这枚硬币,你能否说出每个盒内装的东西呢?
32.吃药问题
某种药方要求非常严格,你每天需要同时服用A、B两种药片各一颗,不能多也不能少。这种药非常贵,你不希望有任何一点的浪费。一天,你打开装药片A的药瓶,倒出一粒药片放在手心;然后打开另一个药瓶,但不小心倒出了两粒药片。现在,你手心上有一颗药片A,两颗药片B,并且你无法区别哪个是A,哪个是B。你如何才能严格遵循药方服用药片,并且不能有任何的浪费?
把手上的三片药各自切成两半,分成两堆摆放。再取出一粒药片A,也把它切成两半,然后在每一堆里加上半片的A。现在,每一堆药片恰好包含两个半片的A和两个半片的B。一天服用其中一堆即可。
33.硬币问题
如何用一枚硬币等概率生成一个1到3之间的随机整数?如果这枚硬币是不公正的呢?
答案:如果是公正的硬币,则投掷两次,“正反”为1,“反正”为2,“正正”为3,“反反”重来。
如果是不公正的硬币,注意到出现“正反”和“反正”的概率一样,因此令“正反反正”、“反正正反”、“正反正反”分别为1、2、3,其余情况重来。另一种更妙的办法是,投掷三次硬币,“正反反”为1,“反正反”为2,“反反正”为3,其余情况重来。
34.灯管问题
在房里有三盏灯,房外有三个开关,在房外看不见房内的情况,你只能进门一次,你用什么方法来区分那个开关控制那一盏灯?
打开一个开关。过10分钟后关掉开关,并打开另一个开关。进屋确认可知:
亮的灯是由第二次打开的开关控制;
摸上去发热的不发亮的灯是由第一次打开的开关控制
剩下的第三盏灯是由未操作过的开关控制。
35.盲人问题
他们都各自买了两对黑袜和两对白袜,八对袜了的布质、大小完全相同,而每对袜了都有一张商标纸连着。两位盲人不小心将八对袜了混在一起。 他们每人怎样才能取回黑袜和白袜各两对呢?
每一对分开,一人拿一只,因为袜子不分左右脚
36.最大钻石问题
一楼到十楼的每层电梯门口都放着一颗钻石,钻石大小不一。你乘坐电梯从一楼到十楼,每层楼电梯门都会打开一次,只能拿一次钻石,问怎样才能拿到最大的一颗?
选择前五层楼都不拿,观察各层钻石的大小,做到心中有数。后面五个楼层再选择,选择大小接近前五层楼出现过最大钻石大小的钻石。
37.飞机飞行的问题
有N架一样的飞机停靠在同一个机场,每架飞机都只有一个油箱,每箱油可使飞机绕地球飞半圈。注意:天空没有加油站,飞机之间只是可以相互 加油。 如果使某一架飞机平安地绕地球飞一圈,并安全地回到起飞时的机场,问:至少需要出动几架飞机? 注:路途中间没有飞机场,每架飞机都必须安全返回起飞时的机场,不许中途降落。
1 | 一共需要6架飞机。假设绕地球一圈为1,3 架飞机同时顺时针飞,在1/8 处 油量为 3/4 3/4 3/4 其中一辆給另外两加满往回飞,此时油量为1,1,到1/4 处 油量为3/4,3/4, 加满一辆,另一辆往回 2/4 ,1,可以飞到3/4 的位置 此时油量为0 |
38.犯人猜颜色
一百个犯人站成一纵列,每人头上随机带上黑色或白色的帽子,各人不知道自己帽子的颜色,但是能看见自己前面所有人帽子的颜色.
然后从最后一个犯人开始,每人只能用同一种声调和音量说一个字:”黑”或”白”,
如果说中了自己帽子的颜色,就存活,说错了就拉出去斩了,
说的答案所有犯人都能听见,
是否说对,其他犯人不知道,
在这之前,所有犯人可以聚在一起商量策略,
问如果犯人都足够聪明而且反应足够快,100个人最大存活率是多少?
答案:这是一道经典推理题
1、最后一个人如果看到奇数顶黑帽子报“黑”否则报“白”,他可能死
2、其他人记住这个值(实际是黑帽奇偶数),在此之后当再听到黑时,黑帽数量减一
3、从倒数第二人开始,就有两个信息:记住的值与看到的值,相同报“白”,不同报“黑”
99人能100%存活,1人50%能活
除此以外,此题还有变种:每个犯人只能看见前面一个人帽子颜色又能最多存活多少人?
答案:在上题基础上,限制了条件,这时上次的方法就不管用了,此时只能约定偶数位犯人说他前一个人的帽子颜色,奇数犯人获取信息100%存活,偶数犯人50几率存活。
39.猴子搬香蕉
一个小猴子边上有100根香蕉,它要走过50米才能到家,每次它最多搬50根香蕉,(多了就被压死了),它每走
1米就要吃掉一根,请问它最多能把多少根香蕉搬到家里。(提示:他可以把香蕉放下往返的走,但是必须保证它每走一米都能有香蕉吃。也可以走到n米时,放下一些香蕉,拿着n根香蕉走回去重新搬50根。)
答案:这种试题通常有一个迷惑点,让人看不懂题目的意图。此题迷惑点在于:走一米吃一根香蕉,一共走50米,那不是把50根香蕉吃完了吗?如果要回去搬另外50根香蕉,则往回走的时候也要吃香蕉,这样每走一米需要吃掉三根香蕉,走50米岂不是需要150根香蕉?
其实不然,本题关键点在于:猴子搬箱子的过程其实分为两个阶段,第一阶段:来回搬,当香蕉数目大于50根时,猴子每搬一米需要吃掉三根香蕉。第二阶段:香蕉数《=50,直接搬回去。每走一米吃掉1根。
我们分析第一阶段:假如把100根香蕉分为两箱。一箱50根。
第一步,把A箱搬一米,吃一根。
第二步,往回走一米,吃一根。
第三步,把B箱搬一米,吃一根。
这样,把所有香蕉搬走一米需要吃掉三根香蕉。
这样走到第几米的时候,香蕉数刚好小于50呢?
100-(n3)<50 && 100-(n-13)>50
走到16米的时候,吃掉48根香蕉,剩52根香蕉。这步很有意思,它可以直接搬50往前走,也可以再来回搬一次,但结果都是一样的。到17米的时候,猴子还有49根香蕉。这时猴子就轻松啦。直接背着走就行。
第二阶段:
走一米吃一根。
把剩下的50-17=33米走完。还剩49-33=16根香蕉。
40.轮流拿石头
问题:一共有N颗石子(或者其他乱七八糟的东西),每次最多取M颗最少取1颗,A,B轮流取,谁最后会获胜?(假设他们每次都取最优解)。
例子:有10个石头,每人每次可以拿1-2个,轮流拿,最后一个拿的人算输,有什么必赢的方案。
先说结论:
假如A先取,N<M,A获胜;
N>M,若N能被(M + 1)整除时,A失败;
若N不能被(M + 1)整除时,A获胜;
假如B先取,(同上);
N>M时,A要想赢,必须要在自己倒数第二次取完的时候还剩下(M + 1)颗石子(此时A和B还可以再取一次就可以分出胜负游戏就结束了),这样不论B取几颗,A都获胜!但是要怎样才能控制最后一轮的石子数量?
分两种情况分析,
- N不能被(M + 1)整除,A先拿走n颗石子(使得剩下的石子数量是(M + 1)的整数倍),那么下一次B拿走k颗石子时,A就拿走(M + 1)- k颗石子。这样不论B怎么拿A总能控制剩下的石子数量是(M + 1)的整数倍,那么最后一轮一定剩下(M + 1)颗石子;
- N能被(M + 1)整除,A就认输吧。。。(B除非傻才会让A赢)无论A怎么拿,B可以控制石子数量(即当B拿完后总能使剩下的石子数量是(M + 1)的整数倍),在最后一轮之前B拿完后还剩(M + 1)颗,A拿多少颗都是输。
https://www.cnblogs.com/StrayWolf/p/5396427.html
答案:较复杂的尼姆博弈:https://blog.csdn.net/BBHHTT/article/details/80199541
母题:有若干堆石子,每堆石子的数量是有限的,二个人依次从这些石子堆中拿取任意的石子,至少一个(不能不取),最后一个拿光石子的人胜利。
1、我们首先以一堆为例: 假设现在只有一堆石子,你的最佳选择是将所有石子全部拿走,那么你就赢了。
2、如果是两堆:假设现在有两堆石子且数量不相同,那么你的最佳选择是取走多的那堆石子中多出来的那几个,使得两堆石子数量相同,这样,不管另一个怎么取,你都可以在另一堆中和他取相同的个数,这样的局面你就是必胜。比如有两堆石子,第一堆有3个,第二堆有5个,这时候你要拿走第二堆的三个,然后两堆就都变成了3个,这时你的对手无论怎么操作,你都可以“学”他,比如他在第一堆拿走两个,你就在第二堆拿走两个,这样你就是稳赢的
41. 蚂蚁走树枝
问题:放N只蚂蚁在一条长度为M树枝上,蚂蚁与蚂蚁之间碰到就各自往反方向走,问总距离或者时间。
答案:这个其实就一个诀窍:蚂蚁相碰就往反方向走,可以直接看做没有发生任何事:大家都相当于独立的
A蚂蚁与B蚂蚁相碰后你可以看做没有发生这次碰撞,这样无论是求时间还是距离都很简单了。
42.三个火枪手
问题:彼此痛恨的甲、乙、丙三个枪手准备决斗。甲枪法最好,十发八中;乙枪法次之,十发六中;丙枪法最差,十发四中。如果三人同时***,并且每人每轮只发一枪;那么枪战后,谁活下来的机会大一些?
答案:
一般人认为甲的枪法好,活下来的可能性大一些。但合乎推理的结论是,枪法最糟糕的丙活下来的几率最大。
那么我们先来分析一下各个枪手的策略。
如同田忌赛马一般,枪手甲一定要对枪手乙先***。因为乙对甲的威胁要比丙对甲的威胁更大,甲应该首先干掉乙,这是甲的最佳策略。
同样的道理,枪手乙的最佳策略是第一枪瞄准甲。乙一旦将甲干掉,乙和丙进行对决,乙胜算的概率自然大很多。
枪手丙的最佳策略也是先对甲***。乙的枪法毕竟比甲差一些,丙先把甲干掉再与乙进行对决,丙的存活概率还是要高一些。
我们根据分析来计算一下三个枪手在上述情况下的存活几率:
第一轮:甲射乙,乙射甲,丙射甲。
甲的活率为24%(40% X 60%)
乙的活率为20%(100% - 80%)
丙的活率为100%(无人射丙)。
由于丙100%存活率,因此根据上轮甲乙存活的情况来计算三人第二轮的存活几率:
情况1:甲活乙死(24% X 80% = 19.2%)
甲射丙,丙射甲:甲的活率为60%,丙的活率为20%。
情况2:乙活甲死(20% X 76% = 15.2%)
乙射丙,丙射乙:乙的活率为60%,丙的活率为40%。
情况3:甲乙同活(24% X 20% = 4.8%)
重复第一轮。
情况4:甲乙同死(76% X 80% = 60.8%)
枪战结束。
据此来计算三人活率:
甲的活率为(19.2% X 60%) + (4.8% X 24%) = 12.672%
乙的活率为(15.2% X 60%) + (4.8% X 20%) = 10.08%
丙的活率为(19.2% X 20%) + (15.2% X 40%) + (4.8% X 100%) + (60.8% X 100%) = 75.52%
通过对两轮枪战的详细概率计算,我们发现枪法最差的丙存活的几率最大,枪法较好的甲和乙的存活几率却远低于丙的存活几率。
43.囚犯拿豆子
问题:有5个囚犯被判了死刑,他们请求上诉,于是法官愿意给他们一个机会。
犯人抽签分好顺序,按序每人从100粒豆子中随意抓取,最多可以全抓,最少可以不抓,可以和别人抓的一样多。
最终,抓的最多的和最少的要被处死。
1、他们都是非常聪明且自私的人。
2、他们的原则是先求保命。如果不能保命,就拉人陪葬。
3、100颗不必都分完。
4、若有重复的情况,则也算最大或最小,一并处死(中间重复不算)。
假设每个犯人都足够聪明,但每个犯人并不知道其他犯人足够聪明。那么,谁活下来的可能性最大?
根据题意,一号知道有五个人抓豆子,为保性命,他只要让豆子在20颗以内就可以了。但是他足够聪明的话他一定拿20颗,因为无论多拿一颗:2,3,4号的人一定会拿20颗最后死的人就会是最多的1号和最少的5号 还是少拿一颗:2,3,4号拿20个后,5号选择也拿20个拉上1234号垫背。(下面会说为什么多拿少拿也只会相差一颗)
2号是知道1号抓了几颗豆子(20)的。那么,对于2号来说,只有2种选择:与1号一样多,或者不一样多。我们就从这里入手。
情况一,假如2号选择与1号的豆子数不一样多,也就是说2号选择比1号多或者比1号少。
我们先要证明,如果2号选择比1号多或者比1号少,那么他一定会选择比1号只多1颗或者只少1颗。
要证明这个并不算太难。因为每个囚犯的第一选择是先求保命,要保命就要尽量使自己的豆子数既不是最多也不是最少。当2号决定选择比1号多的时候,他已经可以保证自己不是最少,为了尽量使自己不是最多,当然比1号多出来的数量越小越好。因为这个数量如果与一号相差大于1的话,那么3号就有机会抓到的居中数,相差越大,二号成为最多的可能性也就越大。反之,当2号决定选择比1号少的时候,也是同样的道理,他会选择只比1号少1颗。既然2号只会会选择比1号多1颗或者比1号少1颗,那么1、2号的豆子数一定是2个连续的自然数,和一定是2n+1(其中1个人是n,另1人是n+1)。
轮到3号的时候,他可以从剩下的豆子数知道1、2号的数量和,也就不难计算出n的值。而3号也只有2个选择:n颗或者n+1颗。为什么呢?这与上面的证明是一样的道理,保命原则,取最接近的数量,这里不再赘述。
不过,3号选择的时候会有一个特殊情况,在这一情况下,他一定会选择较小的n,而不是较大的n+1。这一特殊情况就是,当3号知道自己选择了n后(已保证自己不是最多),剩下的豆子数由于数量有限,4、5号中一定有人比n要少,这样自己一定可以活下来。计算的话就是 [100-(3n+1)]/2<=n ,不难算出,在这个特殊情况下,n>=20。也就是说,当1、2号选择了20或21颗的时候,3号只要选择20颗,就可以保证自己活下来。
这样一来剩下的豆子只剩39颗,4、5号至少有一人少于20颗的(这个人当然是后选的5号),这样死的将是5号和1、2号中选21颗的那个人。当然,1号、2号肯定不会有人选择21这一“倒霉”的数字(因为他们都是聪明人),这样的话,上述“特殊情况(即3号选择n)”就不会发生了。
综上所述,2345这四个人不难从剩下的豆子数知道前面几个人的数量总和,也就不难进而计算出n的值,而这样一来他们也只有n或者n+1这两种选择。最后的5号也是不难算出n的。在前4个人只选择了2个数字(n和n+1)的情况下,5号已是必死无疑,这时,根据“死也要拉几个垫背”的条件,5号会选择n或n+1,选择5个人一起完蛋。
情况二,如果2号选择了与1号不一样多的话,最终结果是5个人一起死,那么2号只有选择与1号一样多了。
那么1、2号的和就是2n,而3号如果选择n+1或者n -1的话,就又回到第一点的情况去了(前3个人的和是3m+1或3m+2),于是3号也只能选择n ,当然,4号还是只能选n,最后的结果仍旧是5个人一起完蛋。
“最后处死抓的最多和最少的囚犯”严格执行这句话的话,除非有人舍己为人,死二留三。但这是足够聪明且自私的囚犯,所以这五个聪明人的下场是全死,这道题只不过是找了一个处死所有人的借口罢了. . . . . .
变种问题:如果每个囚犯都知道其他囚犯足够聪明,事情会怎么发展?
答案:
这样的情况下囚犯一也会像我们一样推导出前面的结论,那么根据自私的规定,他会直接拿完100个,大家一起完蛋(反正结局已定)
44.学生猜生日<笔试高频>
这种题目笔试中出现的次数比较多,用排除法比较好解决
1.
小明和小强都是张老师的学生,张老师的生日是M月N日,
2人都知道张老师的生日是下列10组中的一天,张老师把M值告诉了小明,
把N值告诉了小强,张老师问他们知道他的生日是那一天吗?
3月4日 3月5日 3月8日
6月4日 6月7日
9月1日 9月5日
12月1日 12月2日 12月8日
小明说:如果我不知道的话,小强肯定也不知道.
小强说:本来我也不知道,但是现在我知道了.
小明说:哦,那我也知道了.
请根据以上对话推断出张老师的生日是哪一天?
答案:9月1日
排除法:
1.小明肯定小强不知道是哪天,排除所有月份里有单独日的月份:6月和12月<因为如果小强的M是2或者7的话,小强就知道了,所以把6月7日与12月2日排除>,所以小明拿到的是3或者9
2.小强本来不知道,所以小强拿到的不是2或者7,但是小强现在知道了,说明把6月与12月排除后,小强拿到的是1,4,8中的一个<这里小强肯定没拿到5,否则他不会知道是哪天的>
3.小明现在也知道了,说明小明拿到的不是3,否则他不会知道是3月4日还是3月8日的,所以小明拿到的是9才能唯一确定生日
综上,答案是9月1日
2.
小明和小强是赵老师的学生,张老师的生日是M月N日,张老师
把M值告诉小明,N值告诉小强
给他们六个选项
3月1日 3月3日 7月3日 7月5日
9月1日 11月7日
小明说:我猜不出来
小强说:本来我也猜不出来,但是现在我知道了
问:张老师生日多少
答案:3月1日
排除法:
1.小明说猜不出来,说明小明拿到的不是单独出现的9或者11,说明老师生日只能是3月或者7月
2.小强原本不知道,说明小强拿到的不是单独出现的5或者7,说明老是生日是1日或3日
3.小强现在知道了,说明小强拿到的是1,因为如果拿到的是3,那么小强就不知道是3月3日还是7月3日了
综上,老师生日是3月1日
45.火车开车问题
有一辆火车以每小时15公里的速度离开洛杉矶直奔纽约,另一辆火车以每小时20公里的速度从纽约开往洛杉矶。如果有一只鸟,以外30公里每小时的速度和两辆火车现时启动,从洛杉矶出发,碰到另一辆车后返回,依次在两辆火车来回的飞行,直道两面辆火车相遇,假设洛杉矶到纽约的距离为s, 请问,这只小鸟飞行了多长距离?
那小鸟飞行的距离就是(s/(15+20))*30。 时间 * 速度
